Ammonite was once thought to be the petrified remains of snakes! Modern science, however, tells us that these fascinating fossils are actually the remains of an ancient aquatic mollusk. A mollusk is an invertebrate with a soft, unsegmented body. The soft body of an ammonite was protected by a hard outer shell. The shells of ammonites ranged from an inch to nine feet! Each shell is divided into many different chambers. The walls of each chamber are called septa. The septa were penetrated by the ammonite’s siphuncle, a tube-like structure that allowed the ammonite to control the air pressure inside its shell. Ammonites were aquatic creatures, and being able to control the air pressure inside their shells meant being able to control their buoyancy.
What is the Fibonacci sequence?
The Fibonacci sequence is a list of numbers where every number is the sum of the previous two. The Fibonacci sequence starts at 1 and grows infinitely:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
To put this sequence into mathematical terms, each term Fn = Fn-1 + Fn-2. The Fibonacci sequence can be illustrated geometrically by drawing boxes. The first box should be 1×1, the second box 1×1, the third 2×2, the fourth 3×3, the fifth 5×5, the sixth 8×8, and so on. Each box should be adjacent to the boxes that come before it, forming a spiral of boxes. Have your students create their own Fibonacci squares – graph paper with small boxes works best.
Fibonacci Sequence in Ammonite Fossils
What does ammonite have to do with Fibonacci? Ammonite shells are a naturally occurring example of the Fibonacci sequence. If you draw a quarter circle in each Fibonacci square, they connect to form an ever increasing spiral. Try to find the Fibonacci squares in your ammonite fossils – photocopy the fossil, then start at the very center by drawing two small boxes right next to each other.
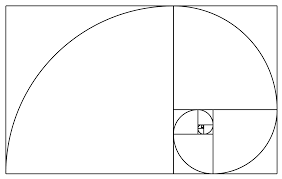
With most fossils, the first boxes are .25 cm by .25 cm. Continue drawing boxes with Fibonacci dimensions. You’ll notice that the spiral of the shell always falls within the Fibonacci squares.
To further examine the concept of the Fibonacci number sequence in nature it is a worthwhile activity to have your students examine plants and flowers. So many of them have leaf structures, petals, and stems that follow the series. These spirals can be seen in everything from sunflowers to pine cones and even pineapples.
If your school doesn’t have access to ammonites, a field trip around the school grounds to identify the Fibonacci sequence in daisies, black-eyed susans, and seed heads would yield many oohs and aahs from your students. The types of explorations are endless as examples of the Fibonacci sequence and the Golden Ratio are, indeed, endless!

Very nice. I have an ammonite fossil. I am not American. I found this fossil in Quezon,Phillipines.
Fascinating. Thank you.